Hebesphenomegacorona
Pronounced /ˈhɛbɪsfɪːnəʊmɛɡəkərəʊnə/
We’re into one of the more arcane areas of three-dimensional geometry here. This figure is a polyhedron, a solid figure with flat faces, specifically an irregular one with 21 faces, 18 of them triangular and the other three square.
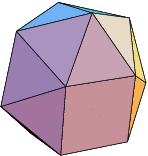
It was given this name in 1966 by Norman W Johnson in an article in the Canadian Mathematical Journal. In this he wrote about the set of three-dimensional solids whose faces are a mixture of triangles, squares, pentagons (5-sides), hexagons (6-sides), octagons (8-sides), and decagons (10-sides).
Two constraints on the solids are that all their edges must be the same length, the faces must be regular, and that there can be no dimples in their surfaces. The technical term for such solids is irregular convex polyhedra. Some of them are complicated, with more than 50 faces. He suggested that there were 92 such solids in all, a result that was proved by Viktor Zalgaller three years later. They are now known as the Johnson solids.
Mr Johnson gave each of the 92 polyhedra a unique name. He explained the term hebesphenomegacorona in his article:
If we define a lune as a complex consisting of two triangles attached to opposite sides of a square, the prefix spheno- refers to a wedgelike complex formed by two adjacent lines. The prefix dispheno- denotes two such complexes, while hebespheno- indicates a blunter complex of two lunes separated by a third lune. The suffix -corona refers to a crownlike complex of 8 triangles, and -megacorona, to a larger such complex of 12 triangles.
These component parts are a mixture of Latin and Greek: hebe is Latin for “blunt”, spheno from the Greek for “wedge”, mega is Greek for “great”, and corona is the Latin for “crown”. So we might translate the word as “large, blunt, wedge-shaped crown”.
Other members of the set have similarly splendid names, such as pentagonal orthocupolarotunda, metabidiminished rhombicosidodecahedron, gyroelongated square dipyramid, gyrobifastigium, pentagonal gyrocupolarotunda, disphenocingulum, and triangular orthobicupola. I will lay heavy odds against you finding any of them in even the largest dictionaries.
[Many thanks to Eric Weisstein for permission to reproduce the image. Pictures of all the Johnson solids are online on his website, together with a wonderful collection of other mathematical information.]
