HEBESPHENOMEGACORONA/ˈhɛbɪsfɪːəʊmɛɡəkərəʊnə/
We’re into one of the more arcane areas of three-dimensional geometry here. This figure is a polyhedron, a solid figure with flat faces, specifically an irregular one with 21 faces, 18 of them triangular and the other three square.
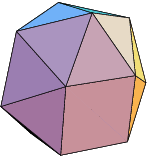
It was given this name in 1969 by Viktor Zalgaller, in an article in which he proved an abstruse result about a set of irregular polyhedra called the Johnson solids. These polyhedra are named after N W Johnson, who had suggested three years earlier that there were just 92 of them. Mr Zalgaller proved this was so and gave each of the 92 polyhedra a unique name. Hebesphenomegacorona can be split into four parts as hebe (from the Latin word for “blunt”), spheno (from the Greek for “wedge”), mega (Greek, “great”), and corona (Latin, “crown”), so making a “large, blunt, wedge-shaped crown”. He came up with many splendid names for other members of the set, like square dipyramid, pentagonal orthocupolarotunda, gyrobifastigium, metabidiminished rhombicosidodecahedron, snub disphenoid, disphenocingulum, pentagonal gyrocupolarotunda, and triangular orthobicupola. I will lay heavy odds against you finding any of them in even the largest dictionaries.
[Many thanks to Eric Weisstein for permission to reproduce the image. Pictures of all the Johnson solids are online, but be prepared for a wait while 92 images download.]
Page created 24 Oct. 1998
Last updated 26 Mar. 2005
